Frivolity: Infinite Turing Machine#
无限图灵机#
(本篇内容倒是很久以前就酝酿在脑子里了……只是一个乱七八糟的猜想,请当我是疯子罢……我发誓再也不搞了,这样下去要变民科叻)
人类已经有很多关于超计算机的设想(超越图灵屏障),并对人脑是否可由机器模拟这类问题悬而未决。
我想试探性把可计算性和不可计算性(不完全地)对偶起来。我认为二者是可以互相涌现的。因此饼的右半部分需要定义一个新的称作无限图灵机 ITM(Infinite Turing Machine),它可以是有无限个带的图灵机、带有概率论意义上的随机的图灵机,或是无限个确定图灵机组成的网络(需要一个函数 \(F\) 来刻画其中的输入输出连结关系),我认为它们是等价的(!)。
Church-Turing Thesis: A function can be calculated by an effective method if and only if it is computable by a Turing machine.
Dual Church-Turing Thesis: A relation can be understanded by an effective way if and only if it is realized by a infinite Turing machine.
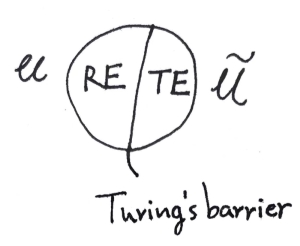
\(RE\) 表示全部图灵可识别语言(Chomsky 形式语法 type-0),\(TE\) 表示 Turing Emergenable(大概需要一个自然语言的语法层级),全部图灵可涌现识别的语言。对应通用图灵机 \(\mathcal{U}\) 的为通用无限图灵机 \(\tilde{\mathcal{U}}\)。(由于至少一种图灵机 \(M_\infty\) 有无限个,我们需要指明输入参数、算法指派的模式作为在无穷网络上的输入。)不仅 \( \tilde{\mathcal{U}} = F(\mathcal{U})\),\(\mathcal{U} = F(\tilde{\mathcal{U}})\) 亦成立。
Descriptive Complexity Thesis:
\(K(M)\) 即描述该 TM 的 Kolmogorov 复杂度,\(\{K,\tilde{K}\}\) 可以称作最佳描述语言;这里有一个对偶。无限计算机之间同样可以进行图灵归约,这个可计算过程应能够映射到对 \(\tilde{K} \in RE\) 的算术操作上来。
左半边的理论 \(Th(\mathcal{M})\)(模型语言 \(\mathcal{M}\) 的真句的集)即我们通俗所谓的理科,能为人所理解,拥有确定而有限的输入和计算过程并给出确定的输出,像一个函数;右半边的理论 \(Th(\tilde{\mathcal{M}})\) 即文科,两者同样因图灵屏障泾渭分明。(BTW,23.10.20 篇我曾自己试图定义 theory,后来发现数理逻辑里有了,应该是等价的)
我不能确定物理理论究竟是否允许不可计算性存在(比如利用大黑洞或量子效应等一大堆构思出的神奇的计算方法)还是可以计算宇宙一切,但目前的人工智能也许都只在(平滑的?)逼近无穷或利用已存的不可计算性。
最后说一些题外话:
当我们实现所谓真正的智能时,那自然再无法奢求可解释性,就像你终究无法预测另一个人一样——而这个社会毕竟建立起来了,建立在人与人相互之间的‘相信’上。为什么说相信不是信任呢?首先人心难料,我们相信的不是别人的善行,而仅仅是别人的行为;更重要的是我们普遍的相信别人有通用的底层的行事逻辑,类似博弈论当中的‘承诺’,比如生命本能的求生欲和繁衍后代的来自基因的任务,让人能够畏惧武力、欺软怕硬,让人能够在社会法律框架下生存并建立契约和信任。
那么智能体同样。(我从来不觉得智能体一定会像计算机一样拥有无处不在的理性,但不妨碍他有逻辑。)
尽管碳基核酸生物和硅基电流生物(这里的‘生物’学和传统的生物学我想应尽快分离开来)的运作模式具有极大差异(电脑病毒或许一下子就蔓延全网电脑了),且从物质性世界上而言二者不在一个‘维度’但能沟通作用(会不会不可计算性就来自于此?)——姑且不论这些,道理可能是正确的:要么让放之共存,要么永不理解。
